library(tidyverse)
library(sandwich)
library(gridExtra)
source("sin_basis_lib.R")
theme_update(text = element_text(size=24))
options(repr.plot.width=12, repr.plot.height=6)Cross validation and variable selection
\(\,\)
Simulated example
# Construct a basis of sin functions of increasing frequency
pmax <- 50
x_grid <- seq(0, 1, length.out=100)
f_mat <- EvalFeatures(x_grid, pmax)
f_names <- colnames(f_mat)
f_df <- data.frame(f_mat) %>%
mutate(x=x_grid) %>%
pivot_longer(cols=(-x)) %>%
mutate(freq=as.numeric(sub("^f", "", name)))
ggplot(f_df %>% filter(freq < 10)) +
geom_line(aes(x=x, y=value, color=name))
n_obs <- 500
sigma_true <- 0.4
models_df <- data.frame()
for (p_true in seq(1, pmax, 7)) {
models_df <-
bind_rows(models_df, DrawData(n_obs, sigma_true, GetBeta(p_true)) %>%
mutate(p_true=p_true))
}#models_df
ggplot(models_df) +
geom_line(aes(x=x, y=ey_true, color=p_true)) +
facet_grid(~ p_true)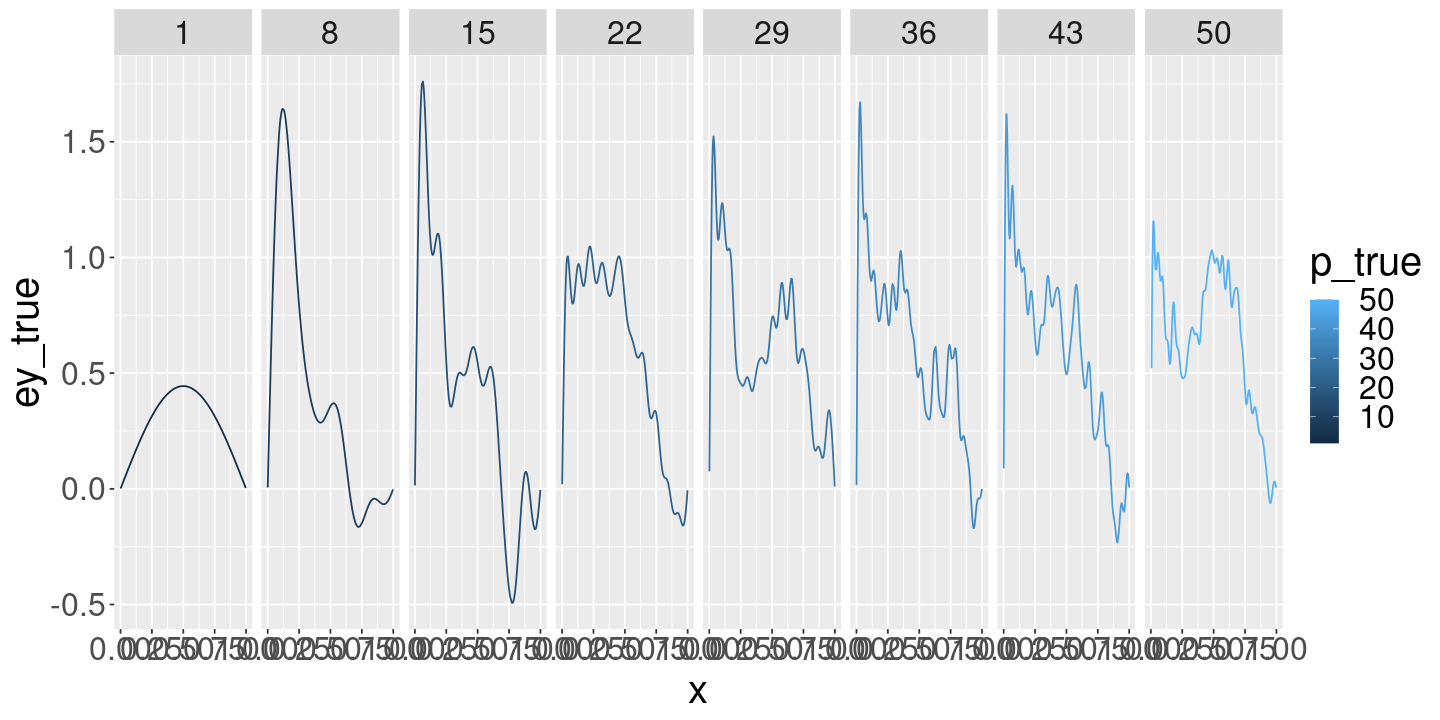
p_true <- 20
beta_true <- GetBeta(p_true)
data_df <- DrawData(n_obs, sigma_true, beta_true)
test_data_df <- DrawData(n_obs, sigma_true, beta_true)
ggplot(data_df) +
geom_line(aes(x=x, y=ey_true)) +
geom_point(aes(x=x, y=y))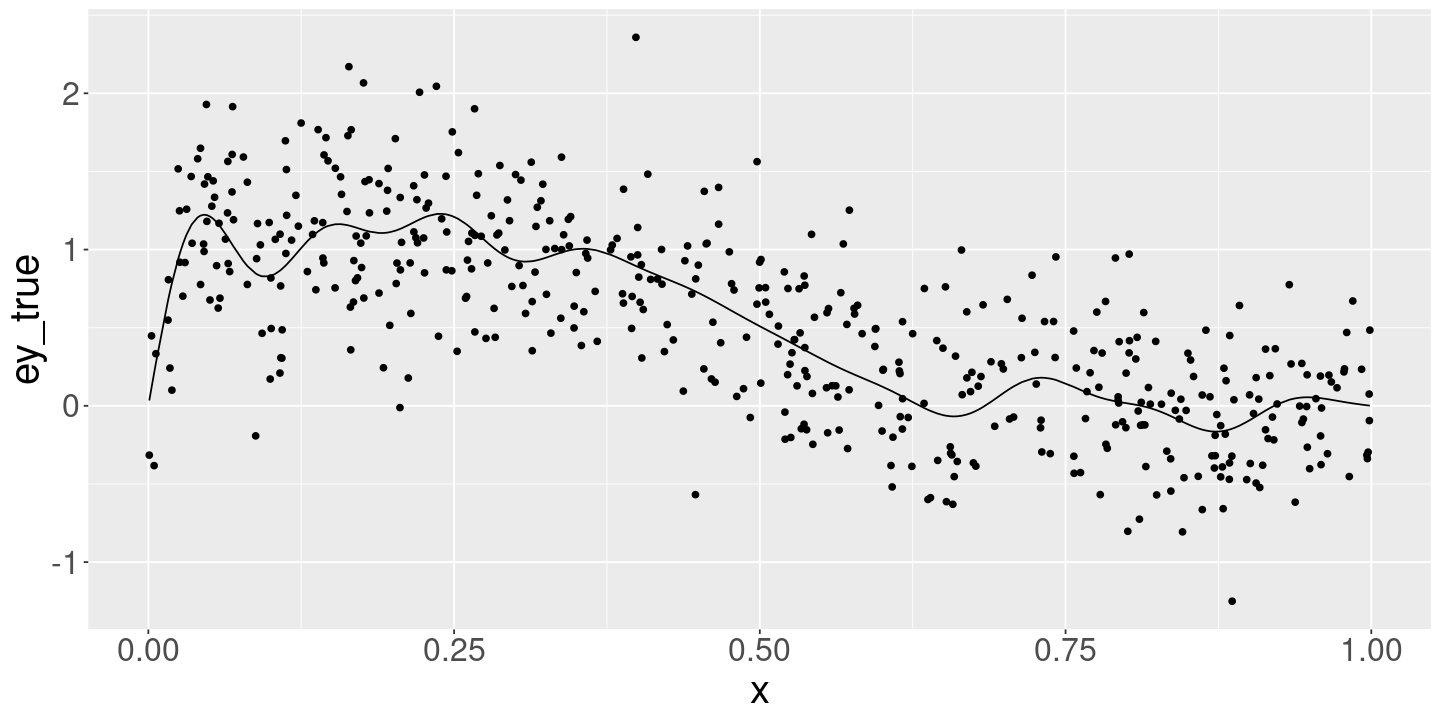
RegressionFormula <- function(p) {
stopifnot(p <= pmax)
form <- sprintf("y ~ -1 + %s", paste(f_names[1:p], collapse=" + "))
return(form)
}
ComputePredictions <- function(data_df, p) {
stopifnot(p <= pmax)
form <- RegressionFormula(p)
lm_fit <- lm(formula(form), data_df)
return(data.frame(y=data_df$y, ey=data_df$ey_true, y_pred=lm_fit$fitted.value, n=data_df$n))
}n_obs <- 500
sigma_true <- 0.4
n_sims <- 20
# Draw multiple datasets with x fixed (so we can estimate bias and variance)
x <- DrawData(n_obs, sigma_true, beta_true)$x
data_df_list <- lapply(1:n_sims, \(s) DrawData(n_obs, sigma_true, beta_true, x=x))
err_df <- data.frame()
# sanity check that all the datasets have the same x
stopifnot(abs((data_df_list[[1]])$x[1] - (data_df_list[[2]])$x[1]) < 1e-8)
p_seq <- unique(c(1, 2, 3, 4, 5, seq(1, pmax, 5)))
pb <- txtProgressBar(min=0, max=n_sims, style=3)
for (sim in 1:n_sims) {
setTxtProgressBar(pb, sim)
for (p in p_seq) {
data_df <- data_df_list[[sim]]
pred_df <- ComputePredictions(data_df, p)
this_err_df <- pred_df %>% mutate(p=p, sim=sim)
err_df <- bind_rows(err_df, this_err_df)
}
}
close(pb) |======================================================================| 100%# Estimate the expectated prediction at each datapoint (to estimate the bias)
err_df <-
err_df %>%
group_by(p, n) %>%
mutate(ey_pn=mean(y_pred)) %>%
ungroup()
# Compute the MSE and related quantities
mse_df <-
err_df %>%
group_by(p) %>%
mutate(pred_err=y_pred - ey,
reg_err=y_pred - ey_pn,
bias=ey_pn - ey) %>%
summarize(mse=mean(pred_err^2),
var=mean(reg_err^2),
bias2=mean(bias^2), # The averaging over new data
rand_err=sigma_true^2) %>%
mutate(mse_check=(mse - (var + bias2)) / mse) # Sanity check -- should be zeromse_df| p | mse | var | bias2 | rand_err | mse_check |
|---|---|---|---|---|---|
| <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> |
| 1 | 0.279678923 | 0.0002413654 | 0.2794375575 | 0.16 | 0.000000e+00 |
| 2 | 0.074893516 | 0.0004585316 | 0.0744349847 | 0.16 | 0.000000e+00 |
| 3 | 0.047569732 | 0.0009167353 | 0.0466529970 | 0.16 | 0.000000e+00 |
| 4 | 0.043212298 | 0.0011564507 | 0.0420558478 | 0.16 | 0.000000e+00 |
| 5 | 0.038724965 | 0.0015370072 | 0.0371879578 | 0.16 | 1.791840e-16 |
| 6 | 0.028645389 | 0.0017793718 | 0.0268660174 | 0.16 | 0.000000e+00 |
| 11 | 0.016470018 | 0.0030544002 | 0.0134156180 | 0.16 | 0.000000e+00 |
| 16 | 0.009757164 | 0.0045852866 | 0.0051718777 | 0.16 | 0.000000e+00 |
| 21 | 0.006371954 | 0.0060273716 | 0.0003445819 | 0.16 | -1.361218e-16 |
| 26 | 0.008059485 | 0.0076840986 | 0.0003753863 | 0.16 | 0.000000e+00 |
| 31 | 0.009651518 | 0.0092509537 | 0.0004005644 | 0.16 | 0.000000e+00 |
| 36 | 0.011174181 | 0.0107215434 | 0.0004526378 | 0.16 | 0.000000e+00 |
| 41 | 0.012872124 | 0.0123678116 | 0.0005043121 | 0.16 | 1.347659e-16 |
| 46 | 0.014374860 | 0.0138330781 | 0.0005417821 | 0.16 | 0.000000e+00 |
mse_graph <- ggplot(mse_df, aes(x=p)) +
geom_line(aes(y=mse, color="MSE")) +
geom_line(aes(y=var, color="var")) +
geom_line(aes(y=bias2, color="bias2")) +
geom_vline(aes(xintercept=p_true), color="purple")
grid.arrange(
mse_graph,
mse_graph + scale_y_log10(),
ncol=2)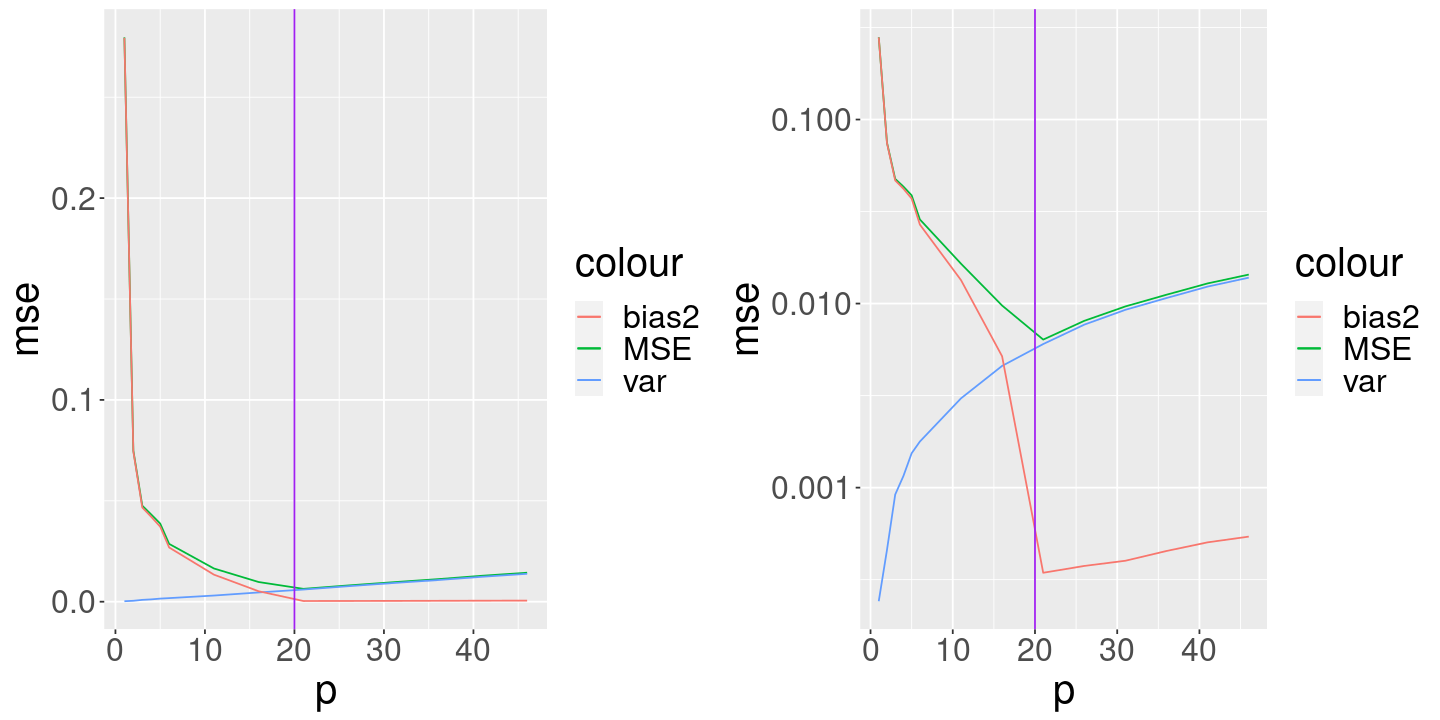
# Perform cross-validation
n_folds <- 10
fold_index <- sample(1:n_folds, n_obs, replace=TRUE)
err_cv_df <- data.frame()
n_data_sets <- length(data_df_list)
stopifnot(n_data_sets <= length(data_df_list))
pb <- txtProgressBar(min=0, max=length(p_seq) * n_data_sets * n_folds, style=3)
pb_ind <- 0
for (p in p_seq) {
for (data_ind in 1:n_data_sets) {
for (fold in 1:n_folds) {
pb_ind <- pb_ind + 1
setTxtProgressBar(pb, pb_ind)
data_df <- data_df_list[[data_ind]] %>% mutate(fold_index=fold_index)
lm_fit <-lm(formula(RegressionFormula(p)), data_df %>% filter(fold_index != !!fold))
data_fold_df <- data_df %>% filter(fold_index == !!fold)
y_pred <- predict(lm_fit, data_fold_df)
mse <- mean((y_pred - data_fold_df$y)^2)
this_err_cv_df <- data.frame(mse=mse, fold=fold, p=p, data_ind=data_ind)
err_cv_df <- bind_rows(err_cv_df, this_err_cv_df)
}}}
close(pb) |================================================================ | 91%err_cv_agg_df <-
err_cv_df %>%
group_by(data_ind, p) %>%
summarize(mse=mean(mse), .groups="keep") %>%
ungroup() %>%
group_by(data_ind) %>%
mutate(is_mse_min=mse <= min(mse))
err_cv_agg_agg_df <-
err_cv_agg_df %>%
group_by(p) %>%
summarize(mse_sd=sd(mse), mse=mean(mse), .groups="drop")
min_ind <- which.min(err_cv_agg_agg_df$mse)
min_mse <- err_cv_agg_agg_df$mse[min_ind]
min_mse_sd <- err_cv_agg_agg_df$mse_sd[min_ind]
min_p <- err_cv_agg_agg_df$p[min_ind]
p_cv <- err_cv_agg_agg_df %>%
filter(mse <= min_mse + min_mse_sd) %>%
pull(p) %>%
min()
print(p_cv)ggplot(err_cv_agg_df, aes(x=p)) +
geom_line(aes(y=mse, group=data_ind, color="CV MSE")) +
geom_line(aes(x=p, y=mse + sigma_true^2, color="True MSE"), data=mse_df, lwd=4) +
geom_point(aes(p, mse), data=filter(err_cv_agg_df, is_mse_min == TRUE)) +
geom_vline(aes(xintercept=p_true)) +
scale_y_log10()
ggplot(err_cv_agg_df, aes(x=p)) +
geom_line(aes(x=p, y=mse, color="Average CV MSE"), data=err_cv_agg_agg_df) +
geom_ribbon(aes(x=p, ymin=mse - mse_sd, ymax=mse + mse_sd), data=err_cv_agg_agg_df, alpha=0.3) +
geom_line(aes(x=p, y=mse + sigma_true^2, color="True MSE"), data=mse_df, lwd=2) +
geom_point(aes(x=p_cv, y=min_mse + min_mse_sd)) +
geom_point(aes(x=min_p, y=min_mse)) +
geom_vline(aes(xintercept=p_true)) +
scale_y_log10()
