$$
\newcommand{\mybold}[1]{\boldsymbol{#1}}
\newcommand{\trans}{\intercal}
\newcommand{\norm}[1]{\left\Vert#1\right\Vert}
\newcommand{\abs}[1]{\left|#1\right|}
\newcommand{\bbr}{\mathbb{R}}
\newcommand{\bbz}{\mathbb{Z}}
\newcommand{\bbc}{\mathbb{C}}
\newcommand{\gauss}[1]{\mathcal{N}\left(#1\right)}
\newcommand{\chisq}[1]{\mathcal{\chi}^2_{#1}}
\newcommand{\studentt}[1]{\mathrm{StudentT}_{#1}}
\newcommand{\fdist}[2]{\mathrm{FDist}_{#1,#2}}
\newcommand{\iid}{\overset{\mathrm{IID}}{\sim}}
\newcommand{\argmin}[1]{\underset{#1}{\mathrm{argmin}}\,}
\newcommand{\projop}[1]{\underset{#1}{\mathrm{Proj}}\,}
\newcommand{\proj}[1]{\underset{#1}{\mybold{P}}}
\newcommand{\expect}[1]{\mathbb{E}\left[#1\right]}
\newcommand{\prob}[1]{\mathbb{P}\left(#1\right)}
\newcommand{\dens}[1]{\mathit{p}\left(#1\right)}
\newcommand{\var}[1]{\mathrm{Var}\left(#1\right)}
\newcommand{\cov}[1]{\mathrm{Cov}\left(#1\right)}
\newcommand{\sumn}{\sum_{n=1}^N}
\newcommand{\meann}{\frac{1}{N} \sumn}
\newcommand{\cltn}{\frac{1}{\sqrt{N}} \sumn}
\newcommand{\trace}[1]{\mathrm{trace}\left(#1\right)}
\newcommand{\diag}[1]{\mathrm{Diag}\left(#1\right)}
\newcommand{\grad}[2]{\nabla_{#1} \left. #2 \right.}
\newcommand{\gradat}[3]{\nabla_{#1} \left. #2 \right|_{#3}}
\newcommand{\fracat}[3]{\left. \frac{#1}{#2} \right|_{#3}}
\newcommand{\W}{\mybold{W}}
\newcommand{\w}{w}
\newcommand{\wbar}{\bar{w}}
\newcommand{\wv}{\mybold{w}}
\newcommand{\X}{\mybold{X}}
\newcommand{\x}{x}
\newcommand{\xbar}{\bar{x}}
\newcommand{\xv}{\mybold{x}}
\newcommand{\Xcov}{\mybold{M}_{\X}}
\newcommand{\Xcovhat}{\hat{\mybold{M}}_{\X}}
\newcommand{\Covsand}{\Sigmam_{\mathrm{sand}}}
\newcommand{\Covsandhat}{\hat{\Sigmam}_{\mathrm{sand}}}
\newcommand{\Z}{\mybold{Z}}
\newcommand{\z}{z}
\newcommand{\zv}{\mybold{z}}
\newcommand{\zbar}{\bar{z}}
\newcommand{\Y}{\mybold{Y}}
\newcommand{\Yhat}{\hat{\Y}}
\newcommand{\y}{y}
\newcommand{\yv}{\mybold{y}}
\newcommand{\yhat}{\hat{\y}}
\newcommand{\ybar}{\bar{y}}
\newcommand{\res}{\varepsilon}
\newcommand{\resv}{\mybold{\res}}
\newcommand{\resvhat}{\hat{\mybold{\res}}}
\newcommand{\reshat}{\hat{\res}}
\newcommand{\betav}{\mybold{\beta}}
\newcommand{\betavhat}{\hat{\betav}}
\newcommand{\betahat}{\hat{\beta}}
\newcommand{\betastar}{{\beta^{*}}}
\newcommand{\betavstar}{{\betav^{*}}}
\newcommand{\loss}{\mathscr{L}}
\newcommand{\losshat}{\hat{\loss}}
\newcommand{\f}{f}
\newcommand{\fhat}{\hat{f}}
\newcommand{\bv}{\mybold{\b}}
\newcommand{\bvhat}{\hat{\bv}}
\newcommand{\alphav}{\mybold{\alpha}}
\newcommand{\alphavhat}{\hat{\av}}
\newcommand{\alphahat}{\hat{\alpha}}
\newcommand{\omegav}{\mybold{\omega}}
\newcommand{\gv}{\mybold{\gamma}}
\newcommand{\gvhat}{\hat{\gv}}
\newcommand{\ghat}{\hat{\gamma}}
\newcommand{\hv}{\mybold{\h}}
\newcommand{\hvhat}{\hat{\hv}}
\newcommand{\hhat}{\hat{\h}}
\newcommand{\gammav}{\mybold{\gamma}}
\newcommand{\gammavhat}{\hat{\gammav}}
\newcommand{\gammahat}{\hat{\gamma}}
\newcommand{\new}{\mathrm{new}}
\newcommand{\zerov}{\mybold{0}}
\newcommand{\onev}{\mybold{1}}
\newcommand{\id}{\mybold{I}}
\newcommand{\sigmahat}{\hat{\sigma}}
\newcommand{\etav}{\mybold{\eta}}
\newcommand{\muv}{\mybold{\mu}}
\newcommand{\Sigmam}{\mybold{\Sigma}}
\newcommand{\rdom}[1]{\mathbb{R}^{#1}}
\newcommand{\RV}[1]{{#1}}
\def\A{\mybold{A}}
\def\A{\mybold{A}}
\def\av{\mybold{a}}
\def\a{a}
\def\B{\mybold{B}}
\def\b{b}
\def\S{\mybold{S}}
\def\sv{\mybold{s}}
\def\s{s}
\def\R{\mybold{R}}
\def\rv{\mybold{r}}
\def\r{r}
\def\V{\mybold{V}}
\def\vv{\mybold{v}}
\def\v{v}
\def\vhat{\hat{v}}
\def\U{\mybold{U}}
\def\uv{\mybold{u}}
\def\u{u}
\def\W{\mybold{W}}
\def\wv{\mybold{w}}
\def\w{w}
\def\tv{\mybold{t}}
\def\t{t}
\def\Sc{\mathcal{S}}
\def\ev{\mybold{e}}
\def\Lammat{\mybold{\Lambda}}
\def\Q{\mybold{Q}}
\def\eps{\varepsilon}
$$
\(\,\)
library (tidyverse)library (sandwich)library (gridExtra)library (glmnet)source ("sin_basis_lib.R" )theme_update (text = element_text (size= 24 ))options (repr.plot.width= 12 , repr.plot.height= 6 )
── Attaching core tidyverse packages ──────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────── tidyverse 2.0.0 ──
✔ dplyr 1.1.2 ✔ readr 2.1.4
✔ forcats 1.0.0 ✔ stringr 1.5.0
✔ ggplot2 3.4.2 ✔ tibble 3.2.1
✔ lubridate 1.9.2 ✔ tidyr 1.3.0
✔ purrr 1.0.1
── Conflicts ────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag() masks stats::lag()
ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors
Attaching package: ‘gridExtra’
The following object is masked from ‘package:dplyr’:
combine
Loading required package: Matrix
Attaching package: ‘Matrix’
The following objects are masked from ‘package:tidyr’:
expand, pack, unpack
Loaded glmnet 4.1-8
See https://glmnet.stanford.edu/articles/glmnet.html
Simulated example
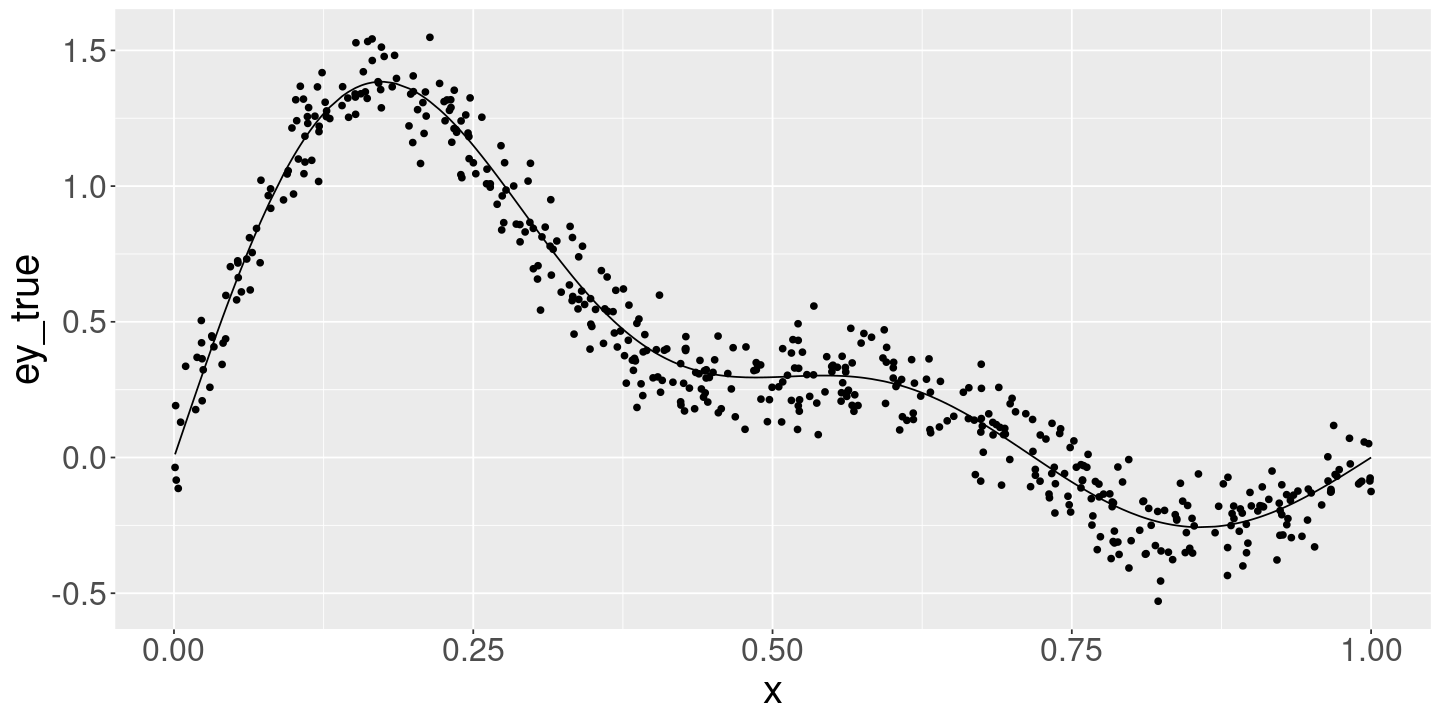
<- 500 <- 0.1 <- 50 <- 5 <- GetBeta (p_true)<- DrawData (n_obs, sigma_true, beta_true)<- DrawData (n_obs, sigma_true, beta_true)ggplot (data_df) + geom_line (aes (x= x, y= ey_true)) + geom_point (aes (x= x, y= y))
if (FALSE ) { <- data_dffor (p in 1 : pmax) {<- paste0 ("f" , p)<- scale (data_norm_df[[fcol]])#cat(mean(data_norm_df[[fcol]]), sd(data_norm_df[[fcol]]), "\n") # sanity check
<- paste (sprintf ("f%d" , 1 : pmax), collapse= " + " )<- paste0 ("y ~ -1 + " , x_reg_form) # glmnet includes a constant <- model.matrix (formula (reg_form), data_df)<- data_df$ y
<- lm (formula (paste0 ("y ~ " , x_reg_form)), data_df)print (summary (lm_fit))
Call:
lm(formula = formula(paste0("y ~ ", x_reg_form)), data = data_df)
Residuals:
Min 1Q Median 3Q Max
-0.249576 -0.070270 -0.002283 0.065265 0.256380
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -5.452e-02 3.883e-02 -1.404 0.16098
f1 5.835e-01 4.998e-02 11.674 < 2e-16 ***
f2 6.107e-01 6.777e-03 90.112 < 2e-16 ***
f3 3.019e-01 1.788e-02 16.886 < 2e-16 ***
f4 3.341e-01 7.002e-03 47.713 < 2e-16 ***
f5 6.752e-02 1.214e-02 5.563 4.57e-08 ***
f6 -4.187e-03 6.695e-03 -0.625 0.53202
f7 1.207e-02 9.796e-03 1.233 0.21840
f8 -1.717e-03 6.819e-03 -0.252 0.80135
f9 7.748e-03 8.735e-03 0.887 0.37553
f10 -5.728e-03 6.946e-03 -0.825 0.41004
f11 1.394e-03 8.165e-03 0.171 0.86451
f12 1.307e-02 6.867e-03 1.904 0.05756 .
f13 -8.012e-03 7.939e-03 -1.009 0.31345
f14 6.892e-03 6.643e-03 1.038 0.30005
f15 7.179e-03 7.461e-03 0.962 0.33646
f16 -9.783e-03 6.962e-03 -1.405 0.16067
f17 6.939e-03 7.366e-03 0.942 0.34669
f18 3.216e-03 7.199e-03 0.447 0.65528
f19 1.223e-02 7.562e-03 1.617 0.10655
f20 -5.658e-03 6.794e-03 -0.833 0.40544
f21 1.157e-02 7.203e-03 1.606 0.10900
f22 -1.865e-03 6.567e-03 -0.284 0.77650
f23 -9.140e-07 7.085e-03 0.000 0.99990
f24 4.233e-03 6.727e-03 0.629 0.52951
f25 1.192e-02 7.360e-03 1.619 0.10617
f26 1.661e-03 6.865e-03 0.242 0.80897
f27 1.177e-02 7.263e-03 1.621 0.10580
f28 8.420e-03 6.807e-03 1.237 0.21676
f29 1.460e-02 7.129e-03 2.049 0.04108 *
f30 -6.379e-03 6.973e-03 -0.915 0.36079
f31 8.061e-03 6.978e-03 1.155 0.24859
f32 -3.400e-03 6.876e-03 -0.494 0.62120
f33 -1.581e-03 7.357e-03 -0.215 0.82998
f34 -7.330e-03 6.891e-03 -1.064 0.28801
f35 1.480e-02 7.063e-03 2.096 0.03666 *
f36 1.188e-03 6.756e-03 0.176 0.86046
f37 -3.304e-03 6.941e-03 -0.476 0.63433
f38 1.904e-02 6.780e-03 2.809 0.00519 **
f39 5.327e-03 7.242e-03 0.735 0.46243
f40 9.430e-03 7.040e-03 1.340 0.18108
f41 3.410e-03 7.031e-03 0.485 0.62790
f42 -1.197e-03 6.936e-03 -0.173 0.86301
f43 6.347e-04 6.890e-03 0.092 0.92664
f44 -6.264e-04 6.753e-03 -0.093 0.92614
f45 7.578e-03 6.892e-03 1.100 0.27207
f46 1.083e-02 6.737e-03 1.608 0.10852
f47 -4.294e-03 7.047e-03 -0.609 0.54264
f48 4.949e-03 6.793e-03 0.729 0.46662
f49 6.476e-03 7.035e-03 0.921 0.35776
f50 1.624e-03 6.683e-03 0.243 0.80807
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.1017 on 449 degrees of freedom
Multiple R-squared: 0.9654, Adjusted R-squared: 0.9616
F-statistic: 250.8 on 50 and 449 DF, p-value: < 2.2e-16
# Interestingly, glmnet with lambda = 0 does _not_ match lm due to differences in the # algorithms. This can be made better (but not to vanish) by changing some # of the parameters. See, e.g., # https://stackoverflow.com/questions/42405362/ordinary-least-squares-with-glmnet-and-lm for (thresh in c (1e-10 , 1e-5 )) { <- glmnet (x, y, alpha= 0 , standardize= TRUE , lambda = rev (0 : 99 ), thres = thresh)<- coef (ridge_fit, s= 0.0 , exact= TRUE ) %>% as.matrix ()<- coef (lm_fit)print (max (abs (beta0_lm - beta0_ridge)))#plot((beta0_ridge), (beta0_lm)); abline(0,1)
[1] 0.0001685906
[1] 0.05290299
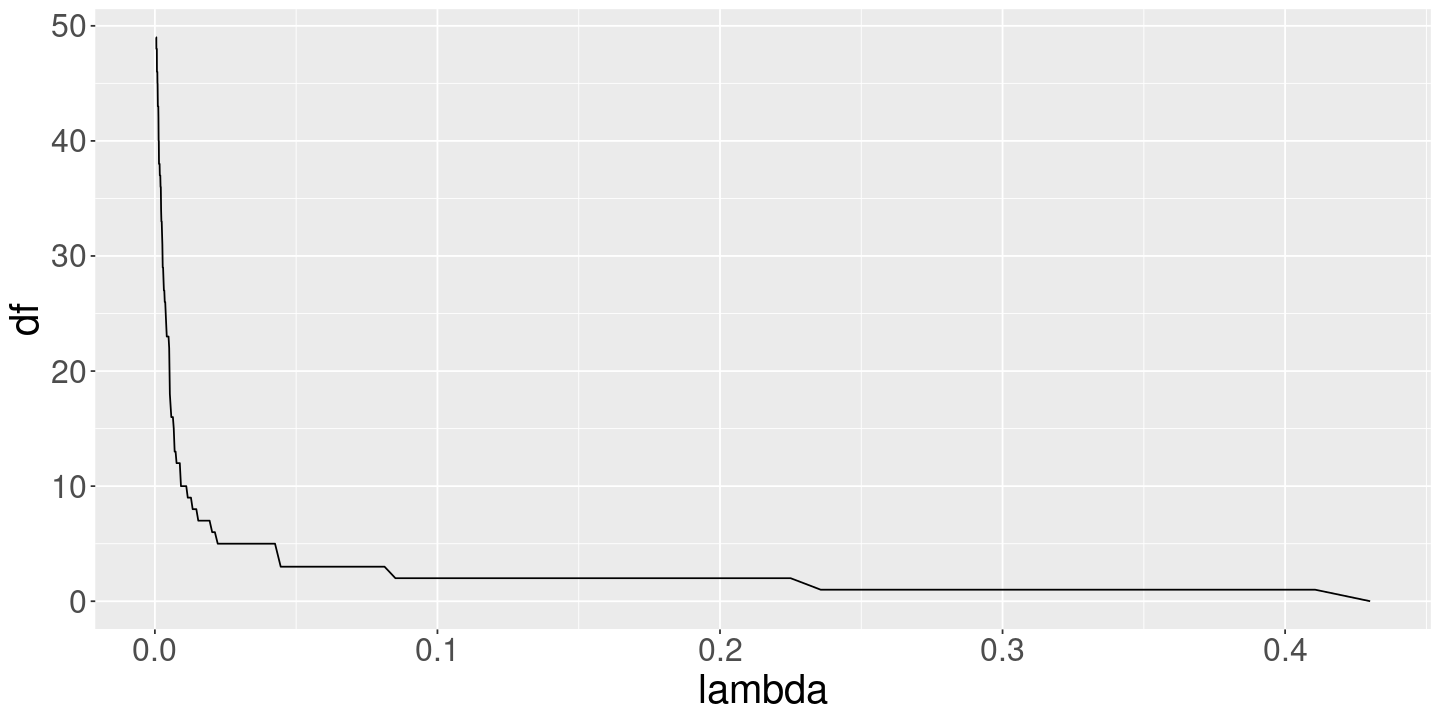
<- glmnet (x, y, alpha= 1 , standardize= TRUE , nlambda= 200 )<- glmnet (x, y, alpha= 0 , standardize= TRUE , nlambda= 200 )
data.frame (lambda= lasso_fit$ lambda, df= lasso_fit$ df) %>% ggplot () + geom_line (aes (x= lambda, y= df))
# glmnet also supports its own cv <- 20 <- cv.glmnet (x, y, alpha= 1 , type.measure= "mse" , nfolds= n_folds)<- cv.glmnet (x, y, alpha= 0 , type.measure= "mse" , nfolds= n_folds)
Call: cv.glmnet(x = x, y = y, type.measure = "mse", nfolds = n_folds, alpha = 1)
Measure: Mean-Squared Error
Lambda Index Measure SE Nonzero
min 0.002830 55 0.01101 0.0004396 29
1se 0.006537 46 0.01140 0.0004224 15
<- function (cv_fit) { <- data.frame ()<- length (cv_fit$ lambda)for (n in 1 : n_lambda) {<- cv_fit$ lambda[n]<- cv_fit$ cvm[n]<- cv_fit$ cvsd[n]<- y - predict (cv_fit, s= lambda, x)<- coef (cv_fit, s= lambda) %>% as.matrix () %>% as.data.frame () %>% rename (beta= s1)$ coef <- rownames (this_coef)$ order <- sub ("^f" , "" , this_coef$ coef) %>% sub (" \\ (Intercept \\ )" , "-1" , .) %>% as.numeric ()<- filter (this_coef, coef != "(Intercept)" ) %>% pull (beta)<- sqrt (sum (beta^ 2 ))<- this_coef %>% mutate (lambda= lambda,cvm= cvm,cvsd= cvsd,df= sum (abs (beta) > 1e-9 ),l2= l2,rss= mean (err^ 2 ))<- bind_rows (coef_df, this_coef)return (coef_df)
<- bind_rows (ExtractCoefficients (lasso_cv_fit) %>% mutate (method= "L1" ),ExtractCoefficients (ridge_cv_fit) %>% mutate (method= "L2" ))
ggplot (coef_df) + geom_line (aes (x= lambda, y= rss)) + scale_x_log10 () + facet_grid (method ~ .)
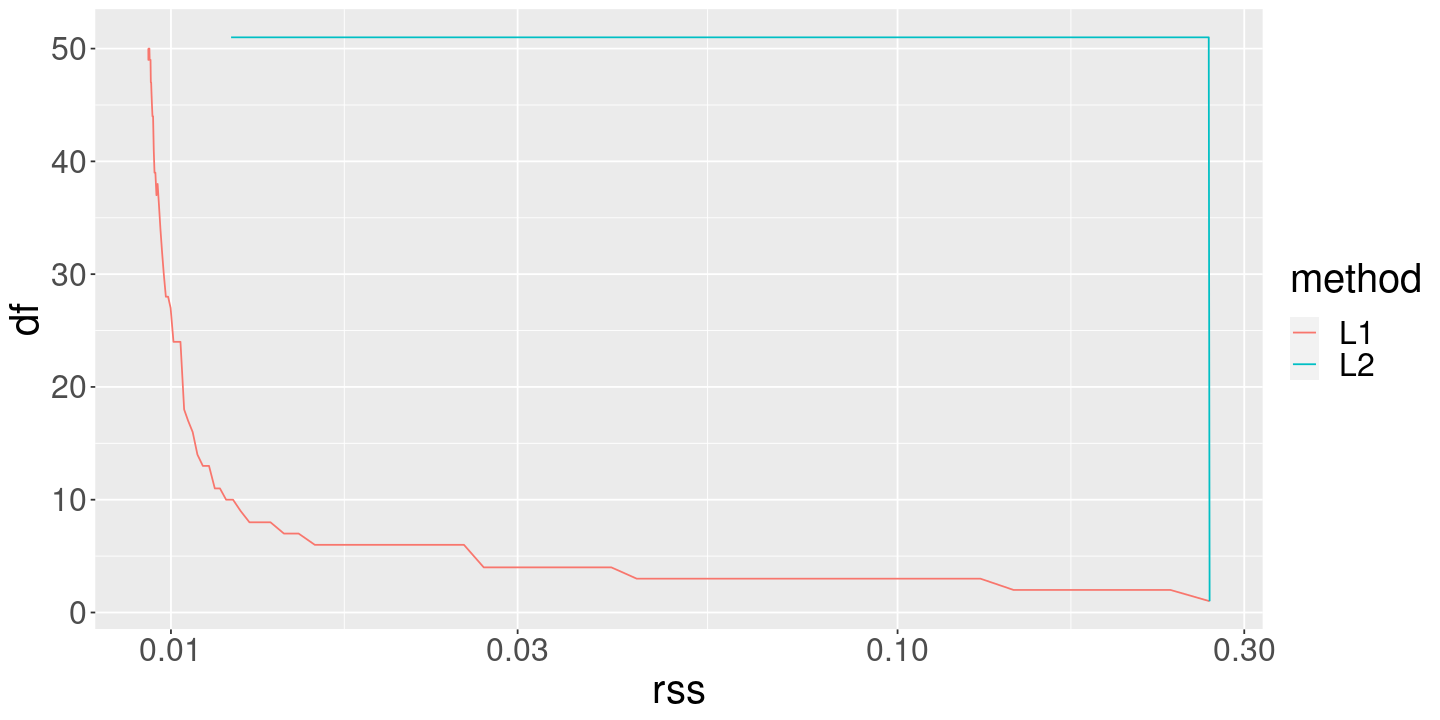
ggplot (coef_df) + geom_line (aes (x= rss, y= df, color= method)) + scale_x_log10 ()
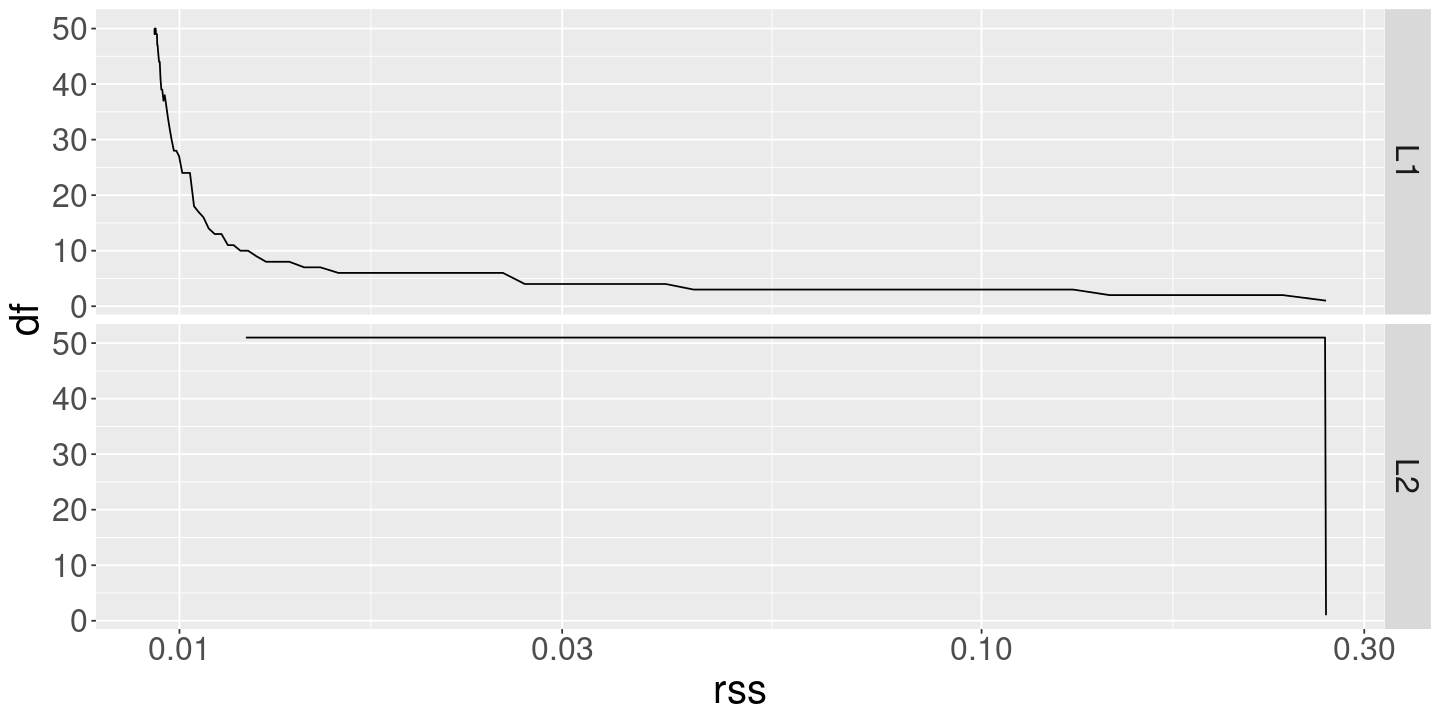
ggplot (coef_df) + geom_line (aes (x= rss, y= df)) + scale_x_log10 () + facet_grid (method ~ .)
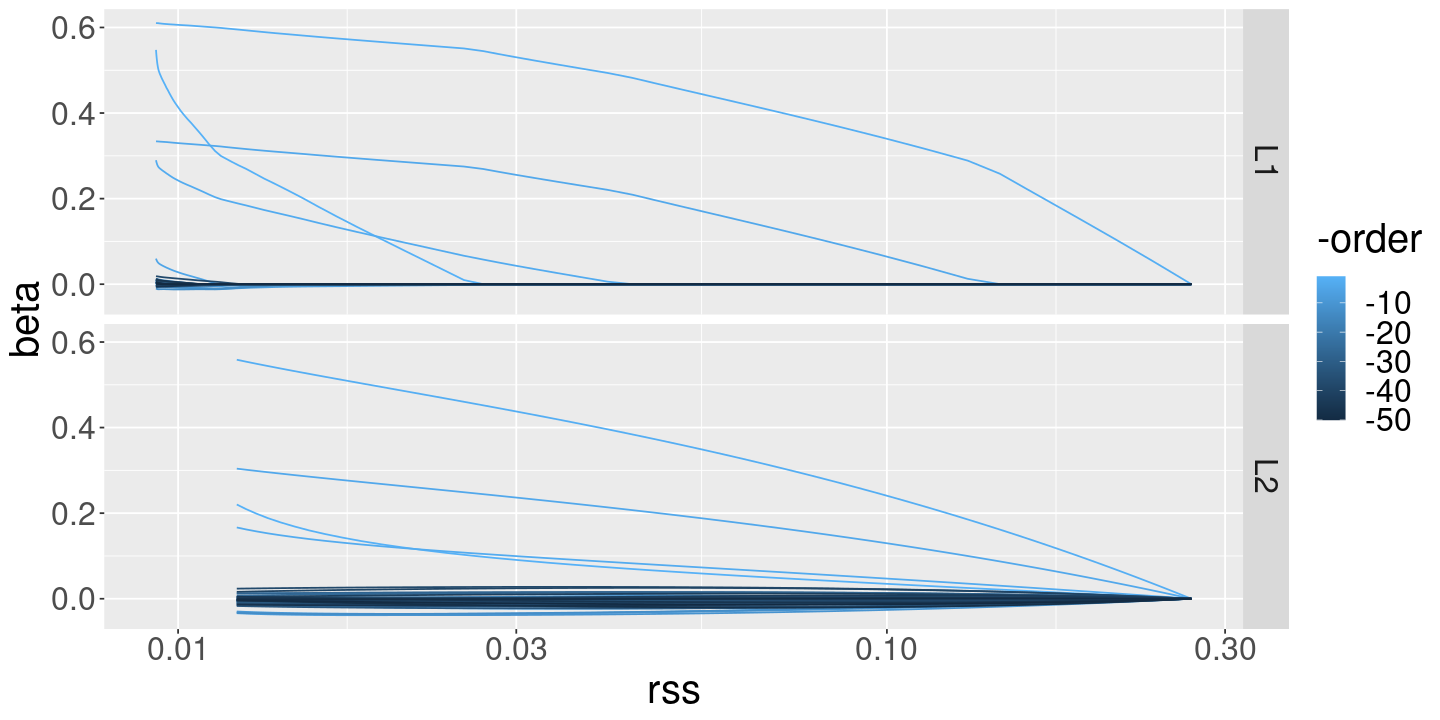
%>% filter (order >= 0 ) %>% ggplot () + geom_line (aes (x= rss, y= beta, color= - order, group= order)) + scale_x_log10 () + facet_grid (method ~ .)
<- coef (lasso_cv_fit, s= lasso_cv_fit$ lambda.min)<- coef (ridge_cv_fit, s= ridge_cv_fit$ lambda.min)<- coef (lasso_cv_fit, s= lasso_cv_fit$ lambda.1 se)<- coef (ridge_cv_fit, s= ridge_cv_fit$ lambda.1 se)cbind (beta_l1, beta_l1_se, beta_l2, beta_l2_se, c (0 , beta_true))
51 x 5 sparse Matrix of class "dgCMatrix"
s1 s1 s1 s1
(Intercept) 0.0559159777 0.1195199729 2.274848e-01 0.2359224816 .
f1 0.4390850048 0.3549208581 2.202358e-01 0.2093368096 0.52255942
f2 0.6071953671 0.6028141264 5.585676e-01 0.5539988948 0.61988711
f3 0.2516674356 0.2200522237 1.665492e-01 0.1619257511 0.27967852
f4 0.3311543933 0.3259580661 3.040330e-01 0.3014332035 0.32116975
f5 0.0340254660 0.0132972595 -5.281719e-03 -0.0072554466 0.05309871
f6 . . -6.945189e-03 -0.0072095864 .
f7 -0.0026578868 -0.0085139392 -3.385000e-02 -0.0347903307 .
f8 . . -1.606844e-03 -0.0016509153 .
f9 -0.0012529750 -0.0034423242 -2.983410e-02 -0.0307354498 .
f10 -0.0015155504 . -1.187068e-03 -0.0008688021 .
f11 -0.0075669189 -0.0093119668 -3.159110e-02 -0.0324857048 .
f12 0.0067830329 . 1.291288e-02 0.0128597642 .
f13 -0.0120912020 -0.0118553166 -3.316692e-02 -0.0336972266 .
f14 0.0011302294 . 5.101317e-03 0.0048819016 .
f15 -0.0002646150 -0.0005460849 -1.565128e-02 -0.0161373052 .
f16 -0.0036409908 . -1.034804e-02 -0.0104750324 .
f17 . . -9.957977e-03 -0.0101079519 .
f18 . . 3.328298e-03 0.0032596125 .
f19 0.0005597877 . -2.416683e-03 -0.0025065729 .
f20 . . -3.804426e-03 -0.0037238308 .
f21 . . -4.324811e-03 -0.0046187905 .
f22 . . -6.855462e-04 -0.0006599058 .
f23 -0.0019957367 . -1.486708e-02 -0.0151850674 .
f24 . . 4.019681e-03 0.0039477908 .
f25 0.0021874932 . -4.423701e-03 -0.0049322025 .
f26 . . 7.195420e-03 0.0075580868 .
f27 0.0039035362 . -3.937927e-03 -0.0044595876 .
f28 0.0038295136 . 1.208542e-02 0.0123099559 .
f29 0.0049526135 . 4.919403e-04 0.0000873082 .
f30 -0.0003634844 . -7.511712e-03 -0.0076679320 .
f31 . . -6.314647e-03 -0.0067335948 .
f32 . . -8.465122e-03 -0.0089055549 .
f33 -0.0055721147 -0.0037906693 -1.691502e-02 -0.0174125577 .
f34 -0.0014670347 . -1.152323e-02 -0.0118947591 .
f35 0.0044580987 . 3.645918e-03 0.0034337109 .
f36 . . 1.809678e-05 -0.0001193806 .
f37 -0.0024203504 . -1.225366e-02 -0.0123540264 .
f38 0.0144596766 0.0087012697 2.358481e-02 0.0238703604 .
f39 . . -4.852247e-03 -0.0051445359 .
f40 0.0052943557 0.0005558600 1.608348e-02 0.0165735894 .
f41 . . -2.944897e-03 -0.0029583128 .
f42 . . 3.792652e-03 0.0041375867 .
f43 . . -4.077957e-03 -0.0039534634 .
f44 . . 3.442316e-04 0.0003759916 .
f45 . . -1.297214e-03 -0.0014757424 .
f46 0.0061767246 0.0002518437 4.682694e-03 0.0042139655 .
f47 -0.0046813835 -0.0009206662 -1.374922e-02 -0.0139922882 .
f48 . . -3.487366e-03 -0.0041390402 .
f49 . . -1.114515e-03 -0.0012250123 .
f50 . . -3.354123e-03 -0.0037306407 .